Understanding Tensile Strength
What is Tensile Strength?
Ultimate tensile strength (UTS), often shortened to tensile strength (TS), is the maximum stress a material can withstand while being stretched or pulled before breaking. In brittle materials, the material breaks soon after reaching the yield point. At the same time, yield strength is observed in ductile materials, and ultimate strength is achieved as the material continues to elongate to the breakpoint.
The chart below shows a ductile material’s elongation (strain) under tensile stress. During the initial stage, elongation is linearly proportional to stress and elastic in nature in that material returns its original length once the stress is removed. The point where strain becomes non-linear to stress is the yield point, and the material elongates more rapidly until the ultimate tensile strength is reached. After the ultimate strength is realized, the material will then neck down until it finally fractures.
The stress-strain curve is less complicated for a brittle material since the material fractures soon after the yield point is observed, and the stress at fracture is the ultimate tensile strength. It is impossible to detect a yield point before ultimate failure in many brittle materials, such as high-strength composites. The material does not undergo a necking period before fracture. The area can see the total energy absorbed by the material under the stress-strain curve. Compared to ductile material, brittle material withstands or absorbs far less energy. Therefore, all of the differences in mechanical behavior between brittle and ductile materials should be considered when designing components and systems.
For ease of comparison between materials, tensile strength/stress is expressed as force (lbf or Newton) divided by the cross-sectional area, i.e., psi (pounds per square inch) or MPa (Newton per square millimeter). One MPa = 145 Psi.
Tensile modulus, modulus of elasticity, or Young’s modulus in tension is the slope (rise/run or stress/elongation) on the initial linear elastic region of the stress/strain curve. It is an important parameter used to compare the stiffness of materials and behavior under stress. The denominator of the rise/run equation is dimensionless, and elongation is often a fraction of a percentage. The unit of modulus is often large, in the Msi or GPa range.
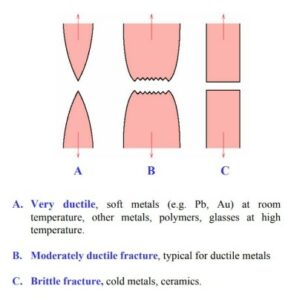
Why is Tensile Strength Important?
Tensile strength is a mechanical property that is often used to determine critical design parameters by engineers. Basic mechanics of materials engineering formulas require tensile strength, and therefore today’s design software also requires this material information. Tensile strength may not always be the critical stress in a design. In fact, some designs may not have any tensile stress. However, tensile strength can also be used as an indicator of other strengths in a material. Engineers can use tensile strength as another indicator of overall material strength when other mechanical properties are unavailable. For example, if fracture toughness is not available, tensile strength can generally indicate if two materials are in the same family (ie-polymeric family).
In many mechanical and structural applications, tensile strength and modulus are important considerations as components are under direct or reactive tensional stress. Also, unlike failures due to fatigue or other mechanical faults, tensile failure could be more sudden and catastrophic, especially with brittle material. Therefore, understanding the ultimate tensile strength and stress-strain behavior (brittle versus ductile) is an important mechanical design consideration.
In electrical applications, mechanical insulation failures can also be catastrophic whether the component supports a live bus or acts as a primary insulator. If a failure of the insulation material occurs, a catastrophic electrical event will most likely happen as a result. Therefore, tensile strength can also be critical in insulation materials used for live support or primary insulation.
Please click here to request access if you are interested in reading the full paper.
